The probability of not receiving the treatment is (1 − p), and therefore the probability of all n patients not receiving the treatment is (1 − p) n , such that the probability of observing at least one patient receiving the treatment is:
These formulae can be used to define a sample size that ensures all key treatments will be observed, and that the proportions can be estimated within desired precision. To utilize them to generate sample size requirements, limited a priori data are required;. n can be selected to yield acceptable values for both quantities. Because the required sample size n increases as p moves further from 0.50, p can be defined to be the most extreme proportion that would be of interest (e.g. a rare treatment given to 1% of the population). Alternatively, sample size requirements can be determined for a range of values of p, or, in situations where the maximum sample size is fixed due to other constraints, the corresponding minimum treatment frequency can be calculated.
Sample size calculations for continuous outcomes (e.g. costs)
When considering medical costs, assuming a normal distribution for mean costs μ and standard deviation σ, precision associated with a particular sample size can be characterized by the width W of the 95% CI:
$$ W=1.96\kern0.5em \times \kern0.5em \frac> $$If an estimate of σ is available, e.g. based on published evidence for another jurisdiction or a similar indication, then the width of the CI can be expressed for the maximum feasible sample size n. Alternatively, Eq. (4) can be rearranged so that the required n can be calculated to obtain 95% CIs for a desired width ± W:
Frequently, estimates of σ aren’t available, making sample size calculations challenging – a challenge common across a variety of contexts when estimating sample size. In the absence of such data, one option is to consider the coefficient of variation cv, defined as \( \frac <\mu >\) . Based on this, σ can be expressed as cv × μ, and for assumed values of cv and μ, n can be estimated without specific estimates for σ. Replacing σ in Eq. (4), the width of a 95% CI can be expressed as:
$$ \pm 1.96\kern0.5em \times \kern0.5em \frac> $$Via this formula, required sample size n can be calculated for a desired with W based on rearranging Eq. (6). If an estimate of μ is available, n can therefore be presented for a desired absolute CI width W Eq. (7). Otherwise, if μ is unknown, the desired width could instead be expressed as a desired percentage of the mean, e.g. it is desired to estimate mean cost with a 95% confidence interval precise to within +/− V% of the mean. This is equivalent to saying that \( \mathrm=\frac<\mathrm
Expressed with respect to absolute width W, the required sample size is:
$$ <\left(\frac<1.96\timesExpressed with respect to width V defined as percentage of the mean, the required sample size is:
A real-world case study is presented below, to describe the precision achieved for a retrospective chart review of burden of illness including treatment patterns and costs in advanced melanoma (the MELODY study) [7], with a total sample size of 655 patients across the United Kingdom (UK), Italy, and France. Costs were presented both per individual overall, as well as per user of specific utilization categories (e.g. hospitalization costs amongst the subgroup with non-zero hospitalization). The range of cv ratios observed in the MELODY study are presented to provide plausible values for future studies.
A sample size calculator based on the formulas presented is available as supplementary material (see Additional file 1).
Results
Based on Eqs. (1–3), Table 1 presents calculated relationships between sample sizes and the expected number of cases to be observed, the probability of observing a treatment in practice, and expected precision, for a range of treatment probabilities. Across sample sizes, any treatment given with greater than 1% frequency has a high likelihood of being observed. For a sample of size 200, and a treatment given to 5% of the population, the precision of a 95% CI is expected to be ±0.03; i.e. the expected 95% CI would be (0.02–0.08). Generally, with respect to characterizing treatment patterns, sample sizes above 200 are only required for treatments given to 1% of the population or less, or if particularly narrow precision estimates are needed. The information in Table 1 can be used to identify the optimal sample size based on a treatment pattern-related research question, or, in the case of a fixed sample size, to identify the level of detail that can be described.
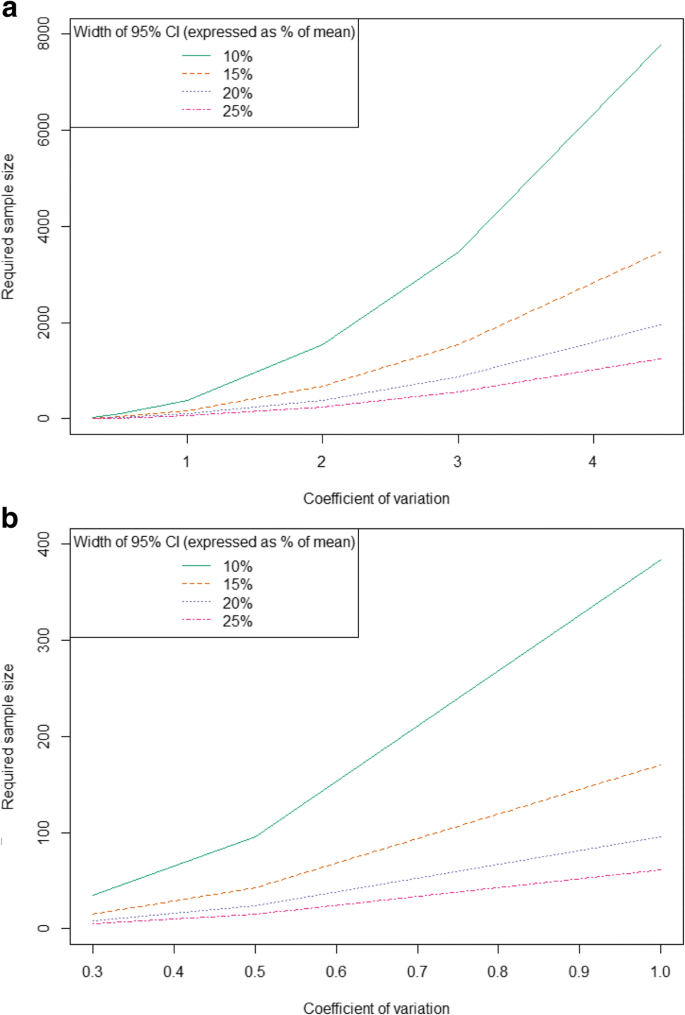
When determining optimal sample size, it is important to consider any subgroups of interest, and either target such subgroups directly in sampling strategy or account for expected sample size needs if only the overall population is to be sampled. For example, if descriptive cost analyses are to be conducted for a sample that is estimated to be 20% of the overall population, and a required sample size is identified based on required precision for this subgroup, the full sample will need to be 1/20% = 5x the required sample size identified by the subgroup.
Discussion
Chart reviews are commonly used to assess clinical outcomes, treatment patterns, and healthcare resource use and costs for more rare health conditions, for very specific indications, or in cases where the required parameters are not captured in large datasets. Despite their ubiquity, methodologic guidance on how to conduct rigorous chart reviews, particularly with respect to selecting appropriate sample sizes, are few. Even the existing methodologic guidance on how to conduct chart reviews provide little direction in this area; suggesting it is beyond the scope of the guidance [6], or assuming a randomized trial-like, hypothesis testing framework [5], rather than methods appropriate for the descriptive objectives that often frame chart reviews. We therefore aimed to fill this gap by providing a framework for estimating appropriate sample sizes for study designs that aim to precisely estimate treatment patterns or resource use parameters, rather than comparing outcomes between groups. These can be especially relevant for situations where the availability of patient charts is limited by time, budget, or the available population size.
We found that for objectives around summarizing categorical and continuous, sample sizes of 100 patients and greater are in most cases sufficient; although larger samples may be required to characterize cost outcomes and/or examine subgroups. For objectives around cost estimation, greater sample sizes are required, particularly if relatively precise estimation is desired, and/or if results specific to particular subgroups are of interest. If 200 to 400 patient charts is the maximum feasible sample size, as is often the case in practice, it can be expected that cost estimate 95% confidence intervals will be precise to within 5–15% of the mean, depending on the ratio of standard deviation to mean costs.
These sample size formulae can be used in two distinct ways. First, if study resources are flexible and desired precision is known, formulae can be used to guide sample size selection. Second, if study resources or available sample size is fixed, formulae can be used to generate anticipated values of precision. We have validated the use of these formulae in a number of other chart review studies [8,9,10]; and have provided this calculator available online for others to use going forward.
This methodological study addresses an important knowledge gap, as sample sizes are frequently determined using ad-hoc approaches and/or based only on feasibility considerations. Indeed, a non-systematic review of ten recently-published chart reviews focusing on assessing treatment patterns and costs revealed that no studies presented a rationale for their chosen sample size [11,12,13,14,15,16,17,18,19,20]. One rule of thumb that has been suggested [6], that is analogous to sample size considerations for regression analyses, is that a minimum of 5–10 charts per variable is required to obtain results that are likely to be both true and clinically useful [21, 22]. However, the number and complexity of outcomes that tend to be considered within a chart review may ultimately limit the utility of this rule in these circumstances, compared to a regression model evaluating the association between a set of independent variables and one dependent variable.
While the methods presented here are broadly applicable to categorical and continuous variables, this does not span the full range of potential outcomes in descriptive burden of illness studies, as resource utilization variables may be analyzed as count data. While a future extension of this work could include formulae based on appropriate distributions (Poisson, negative binomial), the formulas presented for continuous outcomes can be used to generate approximate results based on a normal approximation to the Poisson distribution. For cost data, skewness due to large numbers of zero responses and a few large outlying values may limit the appropriateness of normality assumption; in practice, methods such as two-stage models and/or functional transformations may be undertaken when analyzing data [23]. In sample size estimation, while the assumption of normality for potentially non-normal data is a limitation, using cv values taken from actual cost data will reflect the full scope of variability when such outliers are included and as such are not expected to underestimate required sample size. If doing so yields an infeasibly large sample size, and if statistical techniques are expected to be undertaken at the analysis stage, then this can be incorporated into sample size estimation, e.g. by estimating cv based on a sample with zero-value data points excluded, and/or based on log-transformed data.
The strength of this approach is that it presents a simple, straightforward, validated method for estimating sample size for retrospective studies focusing on multiple descriptive outcomes. In chart reviews, these calculations can be useful during the study design phase, to understand the trade- offs between the expenses in time and money from collecting data from additional charts, versus the additional precision around the estimates that can be obtained. This can be particularly important when considering chart review data as inputs for economic models, where the variability around the estimate can have a major impact. As is the case with estimating sample size a priori for any type of outcome, the applicability of these formulas is limited by the availability of useful preliminary data to use as the basis for the calculations.
A priori estimates of sample size are required when designing chart reviews and other retrospective studies with study objectives that focus on describing treatment patterns, resource use, and costs. However, validated and easily-implemented methods to estimate sample size in this situation are not readily available, or frequently used. The approach presented here is methodologically rigorous and designed for practical application in real-world retrospective chart review studies.
Conclusion
This study presents a formal guidance on sample size calculations for retrospective burden of illness studies. The approach presented here is methodologically rigorous and designed for practical application in real-world retrospective chart review studies and can be used in two distinct ways; where [1] the study resources are flexible and desired precision is known, formulas can be used to guide sample size selection, or [2] if study resources or available sample size is fixed, formulas can be used to generate anticipated values of precision.