Published on 16 September 2022 by Pritha Bhandari. Revised on 6 February 2023.
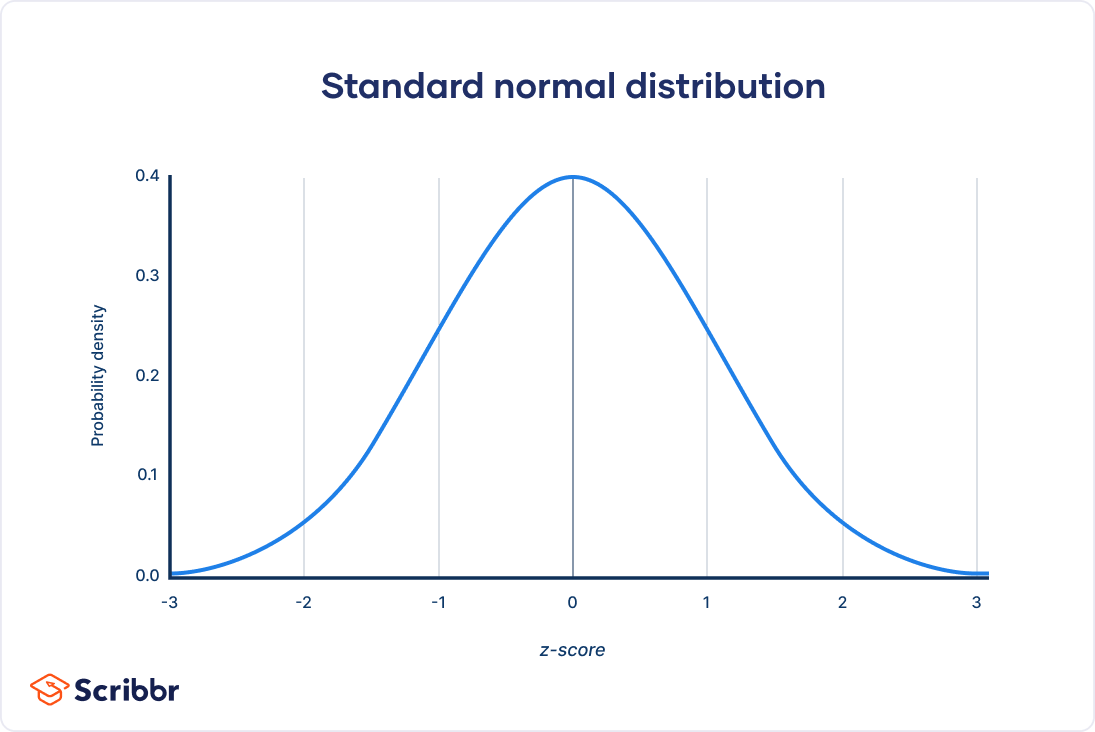
The standard normal distribution, also called the z-distribution, is a special normal distribution where the mean is 0 and the standard deviation is 1.
Any normal distribution can be standardised by converting its values into z-scores. Z-scores tell you how many standard deviations from the mean each value lies.

Converting a normal distribution into a z-distribution allows you to calculate the probability of certain values occurring and to compare different data sets.
You can calculate the standard normal distribution with our calculator below.
All normal distributions, like the standard normal distribution, are unimodal and symmetrically distributed with a bell-shaped curve. However, a normal distribution can take on any value as its mean and standard deviation. In the standard normal distribution, the mean and standard deviation are always fixed.
Every normal distribution is a version of the standard normal distribution that’s been stretched or squeezed and moved horizontally right or left.
The mean determines where the curve is centred. Increasing the mean moves the curve right, while decreasing it moves the curve left.
The standard deviation stretches or squeezes the curve. A small standard deviation results in a narrow curve, while a large standard deviation leads to a wide curve.
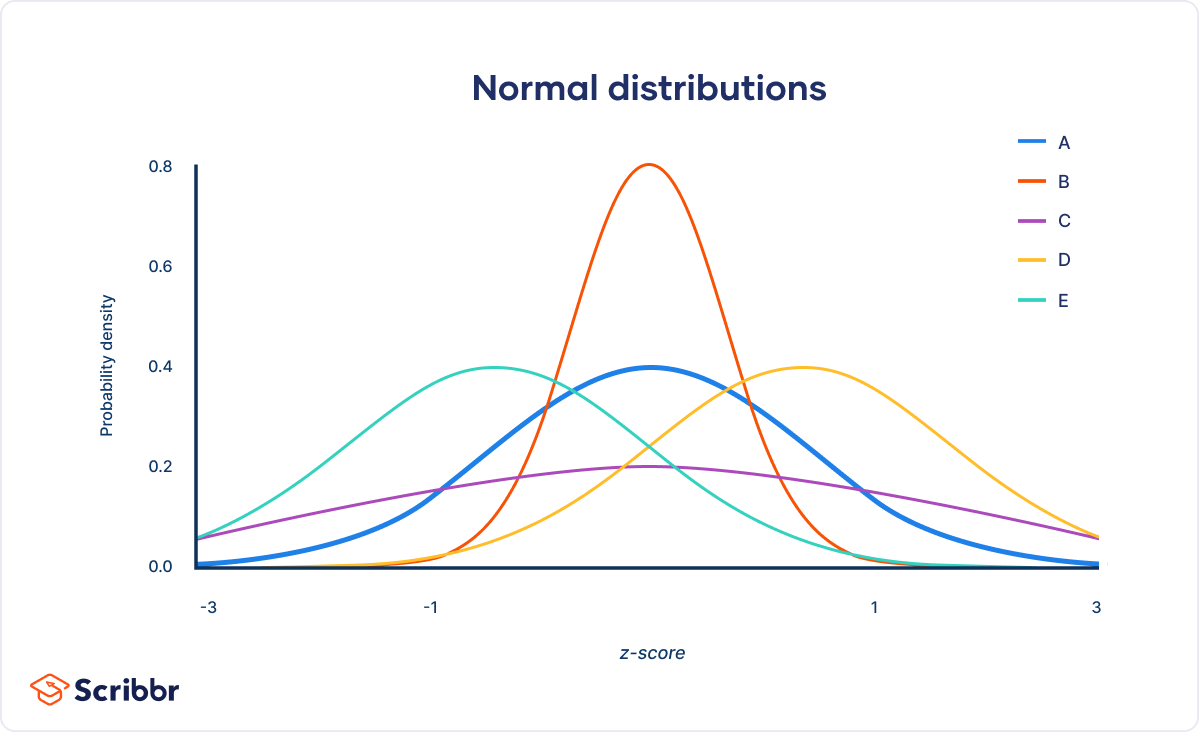
| Curve | Position or shape (relative to standard normal distribution) |
|---|---|
| A (M = 0, SD = 1) | Standard normal distribution |
| B (M = 0, SD = 0.5) | Squeezed, because SD < 1 |
| C (M = 0, SD = 2) | Stretched, because SD > 1 |
| D (M = 1, SD = 1) | Shifted right, because M > 0 |
| E (M = –1, SD = 1) | Shifted left, because M < 0 |
When you standardise a normal distribution, the mean becomes 0 and the standard deviation becomes 1. This allows you to easily calculate the probability of certain values occurring in your distribution, or to compare data sets with different means and standard deviations.
While data points are referred to as x in a normal distribution, they are called z or z-scores in the z-distribution. A z-score is a standard score that tells you how many standard deviations away from the mean an individual value (x) lies:
Converting a normal distribution into the standard normal distribution allows you to:
To standardise a value from a normal distribution, convert the individual value into a z-score:
Let’s walk through an invented research example to better understand how the standard normal distribution works.
As a sleep researcher, you’re curious about how sleep habits changed during COVID-19 lockdowns. You collect sleep duration data from a sample during a full lockdown.
Before the lockdown, the population mean was 6.5 hours of sleep. The lockdown sample mean is 7.62.
To assess whether your sample mean significantly differs from the pre-lockdown population mean, you perform a z-test:
To compare sleep duration during and before the lockdown, you convert your lockdown sample mean into a z-score using the pre-lockdown population mean and standard deviation.
| Formula | Explanation | Calculation |
|---|---|---|
| x = sample mean |
μ = population mean
A z-score of 2.24 means that your sample mean is 2.24 standard deviations greater than the population mean.
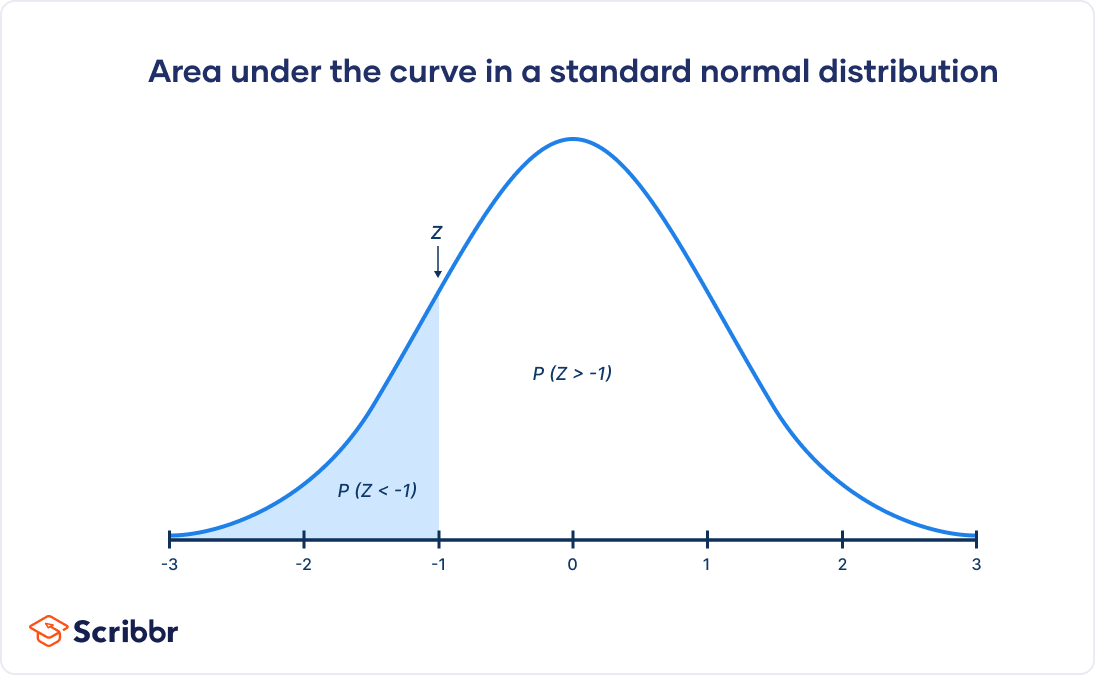
To find the probability of your sample mean z-score of 2.24 or less occurring, you use the z-table to find the value at the intersection of row 2.2 and column +0.04.
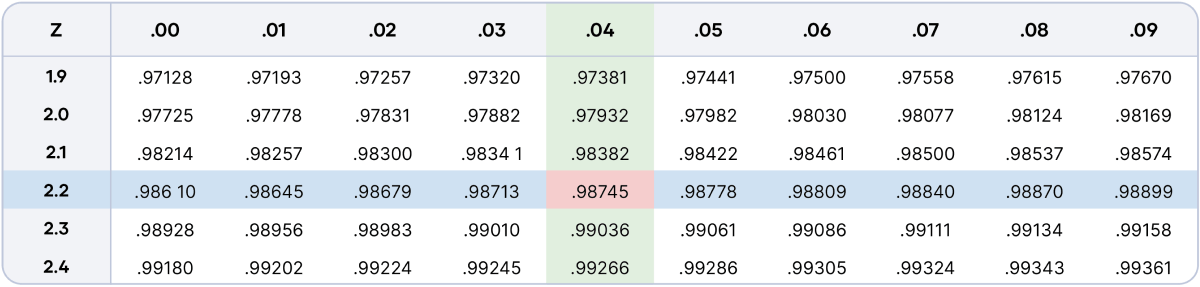
The table tells you that the area under the curve up to or below your z-score is 0.9874. This means that your sample’s mean sleep duration is higher than about 98.74% of the population’s mean sleep duration pre-lockdown.
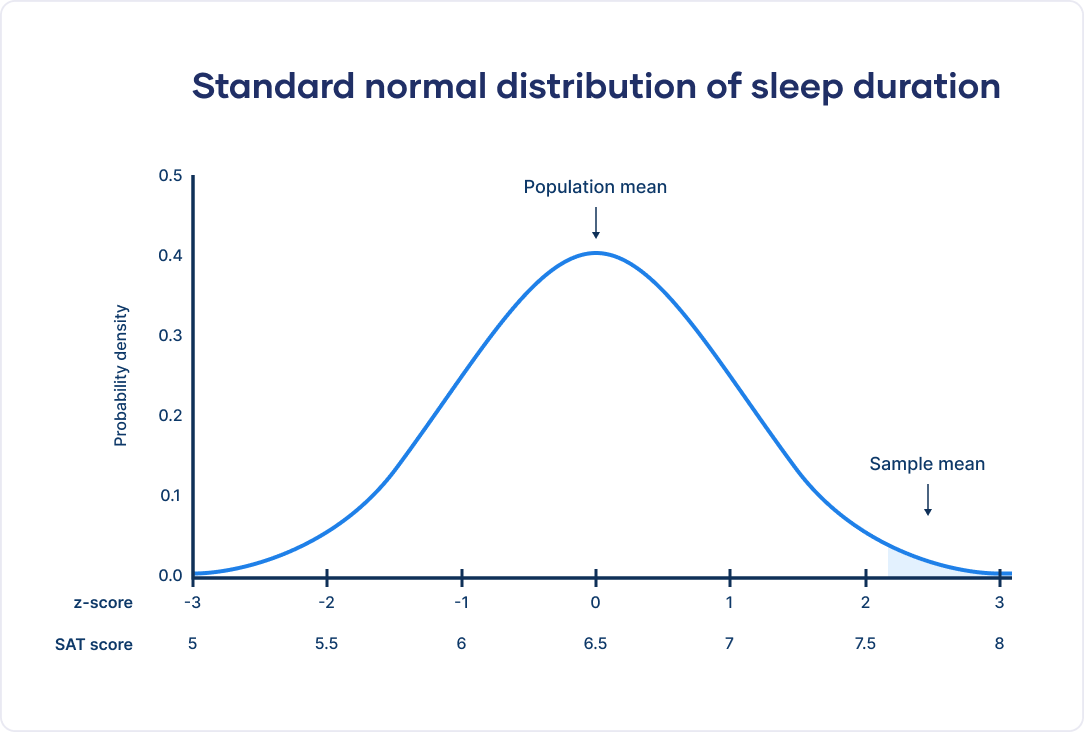
To find the p-value to assess whether the sample differs from the population, you calculate the area under the curve above or to the right of your z-score. Since the total area under the curve is 1, you subtract the area under the curve below your z-score from 1.
A p-value of less than 0.05 or 5% means that the sample significantly differs from the population.
Probability of z > 2.24 = 1 − 0.9874 = 0.0126 or 1.26%
With a p-value of less than 0.05, you can conclude that average sleep duration in the COVID-19 lockdown was significantly higher than the pre-lockdown average.
The t-distribution gives more probability to observations in the tails of the distribution than the standard normal distribution (a.k.a. the z-distribution).
In this way, the t-distribution is more conservative than the standard normal distribution: to reach the same level of confidence or statistical significance, you will need to include a wider range of the data.
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.